Método de Bisección

El método de bisección sigue un enfoque iterativo para reducir progresivamente el intervalo donde puede estar la raíz:

1. Condición inicial: Se elige un intervalo [a,b][a, b] tal que f(a)f(a) y f(b)f(b) tienen signos opuestos, es decir,

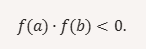
 2.División del intervalo: Se calcula el punto medio cc del intervalo:

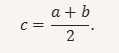
Convergencia y Precisión

Pasos del algoritmo

Ejemplo resuelto paso a paso

Conclusión y aplicación en la vida real

El método de bisección es una herramienta fundamental en el ámbito de los métodos numéricos. Su combinación de robustez, simplicidad y control sobre la precisión lo convierte en un recurso indispensable para ingenieros y científicos a la hora de enfrentar problemas complejos de la vida real. Su uso garantiza aproximaciones confiables, lo que es crucial cuando se trabaja en entornos en los que las soluciones exactas son difíciles de obtener o simplemente inexistentes.