Método de Newton-Raphson

1. Fundamentación del Método

El método de Newton-Raphson se basa en la idea de aproximar una función no lineal mediante su comportamiento lineal en un entorno local. Es decir, se asume que en torno a un estimado inicial xnx_n la función f(x)f(x) puede aproximarse suficientemente bien por una línea tangente. Esta aproximación se justifica mediante el uso de la serie de Taylor, descartando los términos de orden superior y trabajando con la primera aproximación lineal.

1.1. Expansión de Taylor y Aproximación Lineal

Para una función f(x)f(x) que es dos veces diferenciable en un intervalo que contiene la raíz real rr, se puede escribir su expansión de Taylor alrededor de un punto xnx_n de la siguiente forma:

1.2. Interpretación Geométrica

Geométricamente, la aproximación consiste en construir la tangente a la curva y=f(x)y = f(x) en el punto (xn,f(xn))(x_n, f(x_n)) y encontrar el punto donde esa tangente corta el eje xx. La intersección de la tangente con el eje xx (donde y=0y = 0) se toma como la nueva aproximación xn+1x_{n+1}.

Esta estrategia se sustenta en la idea de que la recta tangente es una buena representación local de la función, sobre todo cuando la función es suave y el valor de xnx_n está lo suficientemente cerca de la raíz real. Así, cada iteración ajusta el valor xnx_n a un nuevo valor xn+1x_{n+1} que, en teoría, está más cerca de rr.

1.3. Convergencia Cuadrática y Condiciones

Una de las características más potentes del método de Newton-Raphson es su convergencia cuadrática, bajo las siguientes condiciones:

Inicialización Adecuada: El valor inicial x0x_0 debe ser suficientemente cercano a la raíz rr. Esto garantiza que la aproximación lineal sea válida en la vecindad de rr.
No Nulidad de la Derivada: Se requiere que f′(r)≠0f'(r) \neq 0. Si la derivada en la raíz es cero, la tangente se vuelve horizontal, y la fórmula pierde su significado numérico (se produciría una división por cero o un crecimiento incontrolado del error).
Continuidad y Suavidad: La función f(x)f(x) y su derivada f′(x)f'(x) deben ser continuas en el intervalo considerado. Esto evita comportamientos erráticos y garantiza que la aproximación mediante la tangente sea siempre razonable.

La convergencia cuadrática se expresa en términos del error de la iteración. Sea en=xn−re_n = x_n - r el error en la iteración nn. Bajo las condiciones adecuadas se tiene:

∣en+1∣≈C ∣en∣2,|e_{n+1}| \approx C \, |e_n|^2,

donde CC es una constante relacionada con la segunda derivada de ff. Esto implica que, cuando el método está cerca de la raíz, el número de dígitos correctos se duplica en cada iteración, lo que resulta en una convergencia muy rápida.

1.4. Limitaciones y Consideraciones Prácticas

Si bien el método es muy eficaz, su uso requiere ciertos cuidados:

Elección del Valor Inicial: Un x0x_0 mal escogido puede llevar a divergencia o a converger a una raíz distinta de la esperada.
Derivadas Pequeñas o Nulas: Si en alguna iteración f′(xn)f'(x_n) es muy pequeño o cero, el procedimiento puede volverse inestable o dar saltos grandes en la aproximación, lo que puede hacer que el método no converja.
Funciones No Cuadráticas Localmente: Si la función presenta fuertes no linealidades o inflexiones cerca de la raíz, la suposición de que la función se comporta de manera lineal en ese tramo puede no ser válida, y la convergencia podría ralentizarse o volverse errática.

Pasos del algoritmo

Ejemplo resuelto paso a paso

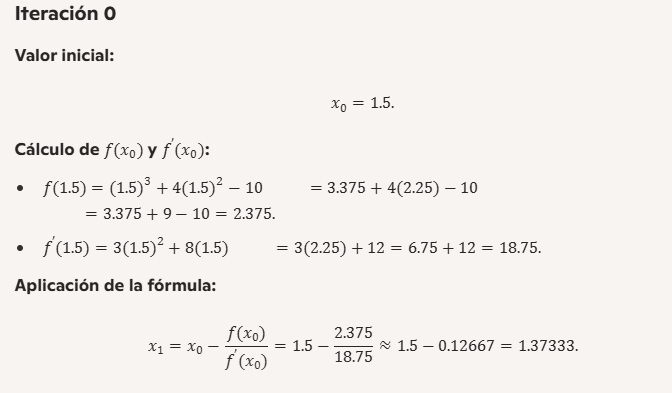
Código del método en Java

public class NewtonRaphson {

// Definición de la función f(x) = x^3 + 4x^2 - 10

public static double f(double x) {

return Math.pow(x, 3) + 4 * Math.pow(x, 2) - 10;

}

// Definición de la derivada f'(x) = 3x^2 + 8x

public static double fPrime(double x) {

return 3 * Math.pow(x, 2) + 8 * x;

}

public static void main(String[] args) {

// Valor inicial

double x0 = 1.5;

// Tolerancia para la convergencia

double tolerance = 1e-6;

// Número máximo de iteraciones

int maxIterations = 100;

int iteration = 0;

double x1 = x0;

System.out.println("Método de Newton-Raphson para f(x)=x^3+4x^2-10");

System.out.println("Valor inicial: x0 = " + x0);

System.out.println();

// Ciclo iterativo para refinar la aproximación

while (iteration < maxIterations) {

double f_x0 = f(x0);

double fPrime_x0 = fPrime(x0);

// Verificar que la derivada no sea cero para evitar división por cero

if (Math.abs(fPrime_x0) < 1e-10) {

System.out.println("La derivada es muy pequeña. El método no puede continuar.");

break;

}

// Aplicar la fórmula iterativa: x1 = x0 - f(x0)/f'(x0)

x1 = x0 - f_x0 / fPrime_x0;

// Imprimir resultados de la iteración actual

System.out.printf("Iteración %d: x0 = %.6f, f(x0) = %.6f, x1 = %.6f%n",

iteration, x0, f_x0, x1);

// Verificar convergencia: se puede usar la diferencia entre iteraciones o el valor de f(x1)

if (Math.abs(x1 - x0) < tolerance) {

break;

}

// Actualizar el valor para la siguiente iteración

x0 = x1;

iteration++;

}

System.out.printf("%nLa raíz aproximada es: x = %.6f%n", x1);

System.out.printf("f(x) en la raíz aproximada es: %.6f%n", f(x1));

System.out.println("Número de iteraciones: " + iteration);

}

Conclusión sobre su uso y aplicación en la vida real

El método es ampliamente valorado en la práctica debido a su rapidez y precisión al resolver ecuaciones no lineales. Algunas conclusiones sobre su uso en la vida real son:

Eficiencia y Convergencia Cuadrática: Una de las principales fortalezas del método es su convergencia cuadrática, lo que implica que, una vez que se está cerca de la raíz, el número de dígitos correctos normalmente se duplica con cada iteración. Esto permite obtener soluciones muy precisas en pocas iteraciones, siendo especialmente útil en aplicaciones donde el tiempo y la precisión son críticos.
Uso en Diversas Disciplinas: Gracias a su rapidez y la facilidad de integración en algoritmos computacionales, el método de Newton-Raphson se emplea en numerosos ámbitos, como la ingeniería (por ejemplo, en análisis de circuitos, mecanismos y sistemas de control), en física (para resolver ecuaciones de movimiento o equilibrio) y en optimización de modelos matemáticos complejos. Además, resulta indispensable en el desarrollo de simulaciones numéricas, donde encontrar raíces de ecuaciones de forma repetitiva se vuelve recurrente.
Importancia de la Conocimiento del Comportamiento Local: Al apoyarse en la derivada de la función, el método aprovecha la información de la pendiente para ajustar la estimación de la raíz. Esta propiedad permite una adaptación rápida a cambios locales en el comportamiento de la función, lo cual es vital en problemas donde la linealidad local es una buena aproximación de la función compleja.
Limitaciones y Consideraciones Prácticas: Si bien el método es muy potente, su exitoso empleo depende en buena medida de la elección de un valor inicial adecuado y de que la función y su derivada sean lo suficientemente suaves en el entorno de la raíz. En casos donde se presentan derivadas cercanas a cero o se elige un valor inicial distante de la solución, el método puede divergent o tardar en converger, lo que exige un análisis preliminar del problema y, en ocasiones, la utilización de métodos híbridos o técnicas de refinamiento.

En conclusión, el método de Newton-Raphson se destaca en la vida real por su capacidad para proporcionar soluciones de alta precisión de forma rápida y con un costo computacional relativamente bajo, siempre que se cumplan sus requisitos teóricos. Estas características lo convierten en una herramienta indispensable para ingenieros y científicos, facilitando el análisis, el diseño y la simulación de sistemas complejos en los que las soluciones exactas no son factibles de obtener de manera directa.